МАТЕМАТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ КОМПОЗИЦИИ
Еще в глубокой древности человеком было обнаружено, что все явления в природе связаны друг с другом, что все пребывает в непрерывном движении, изменении, и, будучи выражено числом, обнаруживает удивительные закономерности. В Древней Греции эпохи классики возник ряд учений о гар монии. Из них наиболее глубокий след в мировой культуре оставило Пифагорейское учение. Последователи Пифагора представляли мир, вселенную, космос, природу и человека как единое целое, где все взаимосвязано и находится в гармонических отношениях. Гармония здесь выступает как начало порядка — упорядочивания хаоса. Гармония присуща природе и искусству: «Одни и те же законы существуют для музыкальных ладов и планет». Пифагорейцы и их последователи всему сущему в мире искали числовое выражение. Ими было обнаружено; что математические пропорции лежат в основе музыки (отношение длины струны к высоте тона, отношения между интервалами, соотношение звуков в аккордах, дающих гармоническое звучание). Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что а основе мироздания лежат симметричные геометрические формы.
Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую «Канон». Все классическое искусство Греции носит печать пифагорейского учения о про порциях. Его влияние испытали на себе ученые средневековья, наука и искусство эпохи Возрождения, Нового времени вплоть до наших дней. Вслед за пифагорейцами средневе-ковый ученый Августин назвал красоту «числовым равенством». Философ схоласт Бонавентура писал: «Красоты и наслаждения нет без про-
порциональности, пропорциональность же прежде всего существует в числах. Необходимо, чтобы все поддавалось счислению». Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: «Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона по- знает ученый».14
Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.
Пропорция означает равенство двух или нескольких отношений. Существует несколько видов пропорциональности: математическая, гармоническая, геометрическая и др. В математической равенство двух отношений выражается формулой a:b=с:d, и каждый член ее может быть определен через остальные три. В гармонической пропорции 3 элемента. Они являются или попарными разностями некоторой тройки элементов, или самими этими элементами, например: а:с=(а — в): (в — с).
В геометрической пропорции тоже всего 3 элемента, но один из них общий, а:в=в:с. Разновидностью геометрической пропорции является пропорция так называемого «золотого сечения», имеющая всего два члена — «а» и «в» — излюбленная пропорция художников, которую в эпоху Возрождения называли «божественной пропорцией».
Золотое сечение (з. с.) Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е. а:в=в: (а — в). Отношение з. с. выражается числом 0,618. Пропорция з. с. 1:0,618=0,618:0,382.
Если, отрезок прямой выразить через единицу, а затем разделить его на два отрезка по з. с., то больший отрезок будет равен 0,618, а меньший 0,382. На рис. 7 показано деле ние отрезка на части по з. с.
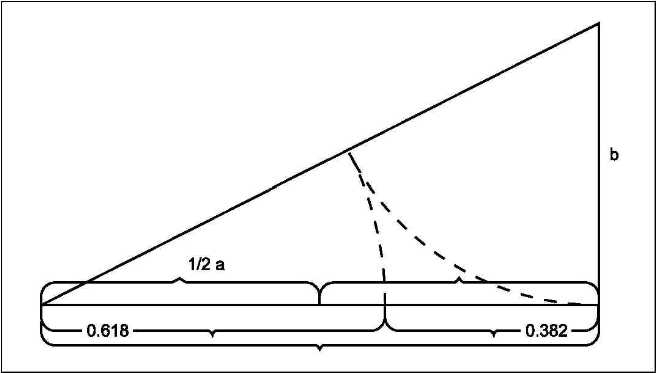
На основании пропорции з. с. был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством что, отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к О,б18, то есть, к отношению з. с.Пропорции з. с. ученые связывают с развитием органической материи. з. с. было обнаружено в объектах живой природы — в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его на блюдали в устройстве вселен ной в расположении планет. В отношении з. с. находятся так же элементы геометрических фигур — пятиугольника, звезды. (Рис. 8.).В прямоугольнике з. с. (р 9, 10) стороны находятся в отношении з.с. Этот пр-к содержит в себе квадрат и малый пр-к з. с. (его большая сторона является малой стороной первоначального пр-ка.) Поэтому можно построить пр-к з.с. на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится пр-к з.с., как показано на рис
Этот малый пр-к подобен большому пр-ку, со-ставленному из квадрата и малого пр-ка з. с., то есть оба эти пр-ка являются пр-ка з. с.Иначе говоря, если отсечь от пр-ка з. с.. квадрат, то остается меньший пр-к, стороны которого опять же будут находиться в отношении з. с. Разбивая этот меньший пр-к на квадрат и еще меньший пр-к, мы опять получим пр-к з. с., и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют «кривая развития», «спираль жизни», ибо в ней как бы заложена идея бесконечного развития.
Бесконечное повторение пр-ка з. с. и квадрата при рассечении пр-ка з. с. обнаруживает повто-рение целого в его частях, что является одним из условий гармонии целого. Это свойство пр-ка з. с. было обнаружено художниками и они стали употреблять з. с. как способ гармонизации, способ пропорционирования. Фидий использовал з. с. при постройке Акрополя (5 век до н. э.) Греческие ремесленники, создавая гончарные изделия также применяли з. с. В эпоху Возрождения з. с. использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли з. с. в поисках гармоничных пропорций букв. (Рис 12),Пр-к з. с. мы встречаем и в пропорциях средневековых рукописных книг, и в современной книге, так как стройные пропорции з. с. позволяют красиво организовать пространство книжной страницы и разворота Пропорционирование — при ведение частей целого к единому пропорциональному строю.В ХХ веке вновь возродился интерес к золотому сечению как к способу пропорционирования. Оно привлекло внимание архитекторов. Советский архитектор Жолтовский и француз Корбюзье занимались проблемами з. с. и использовали его в своей архитектурной практике, Корбюзье создал целую систему пропорционирования на основе чисел ряда золотого сечения и пропорций человеческого тела и назвал ее «Модулор», что по-латыни означает- ритмически размерять Модулор Корбюзье представляет собой гармонические ряды чисел, которые связаны в единую систему и предназначены для использования в архитектуре и дизайне — для гармонизации всей среды, в которой обитает человек. Корбюзье мечтал о перестройке с помощью Модулора всей архитектурной и предметной среды. Сам он создал несколько прекрасных образцов архитектуры, но о более широком применении Модулора в существующих условиях не могло быть и речи. Модулор использовался в ряде слуйаев в дизай¬не и в графическом дизайне — при конструиро¬вании печатных изданий. На рис. 16 приводятся варианты деления прямоугольника 3:4, приведенные Корбюзье для демонстрации возможностей конструирования с помощью Модулора.В разработку вопроса пропорционирования и ис-пользования золотого сечения нес свой вклад Д. Хэмбидж. В 20-м году в Нью-Йорке вышла его книга «Элементы динамической симметрии». Хэмбидж исследовал динамическую симметрию, которую он обнаружил в ряде прямоугольников, с целью ее практического применения художниками в композиционном построении. Он делает попытку раскрыть секреты, которыми пользовались древние греки, добиваясь гармонического решения формы. Его внимание привлекли свойства прямоугольников, составляющих ряд, где каждый последующий прямоугольник строится на диагонали предыдущего, начиная с диагона-ли квадрата Ц2. Это прямоугольники Ц4, Ц5 (с меньшей стороной равной стороне квадрата, принятой за единицу). (Рис. 17). Кульминацией ряда является прямоугольник Ц5, обладающий особыми гармоническими свойствами и «родственный» прямоугольнику золотого сечения, (о нем будет сказано ниже).<
Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую «Канон». Все классическое искусство Греции носит печать пифагорейского учения о про порциях. Его влияние испытали на себе ученые средневековья, наука и искусство эпохи Возрождения, Нового времени вплоть до наших дней. Вслед за пифагорейцами средневе-ковый ученый Августин назвал красоту «числовым равенством». Философ схоласт Бонавентура писал: «Красоты и наслаждения нет без про-
порциональности, пропорциональность же прежде всего существует в числах. Необходимо, чтобы все поддавалось счислению». Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: «Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона по- знает ученый».14
Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.
Пропорция означает равенство двух или нескольких отношений. Существует несколько видов пропорциональности: математическая, гармоническая, геометрическая и др. В математической равенство двух отношений выражается формулой a:b=с:d, и каждый член ее может быть определен через остальные три. В гармонической пропорции 3 элемента. Они являются или попарными разностями некоторой тройки элементов, или самими этими элементами, например: а:с=(а — в): (в — с).
В геометрической пропорции тоже всего 3 элемента, но один из них общий, а:в=в:с. Разновидностью геометрической пропорции является пропорция так называемого «золотого сечения», имеющая всего два члена — «а» и «в» — излюбленная пропорция художников, которую в эпоху Возрождения называли «божественной пропорцией».
Золотое сечение (з. с.) Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е. а:в=в: (а — в). Отношение з. с. выражается числом 0,618. Пропорция з. с. 1:0,618=0,618:0,382.
Если, отрезок прямой выразить через единицу, а затем разделить его на два отрезка по з. с., то больший отрезок будет равен 0,618, а меньший 0,382. На рис. 7 показано деле ние отрезка на части по з. с.

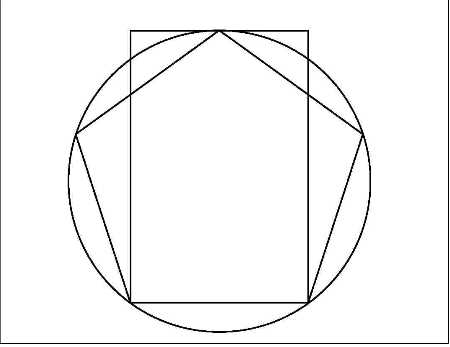
На основании пропорции з. с. был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством что, отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к О,б18, то есть, к отношению з. с.Пропорции з. с. ученые связывают с развитием органической материи. з. с. было обнаружено в объектах живой природы — в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его на блюдали в устройстве вселен ной в расположении планет. В отношении з. с. находятся так же элементы геометрических фигур — пятиугольника, звезды. (Рис. 8.).В прямоугольнике з. с. (р 9, 10) стороны находятся в отношении з.с. Этот пр-к содержит в себе квадрат и малый пр-к з. с. (его большая сторона является малой стороной первоначального пр-ка.) Поэтому можно построить пр-к з.с. на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится пр-к з.с., как показано на рис
Этот малый пр-к подобен большому пр-ку, со-ставленному из квадрата и малого пр-ка з. с., то есть оба эти пр-ка являются пр-ка з. с.Иначе говоря, если отсечь от пр-ка з. с.. квадрат, то остается меньший пр-к, стороны которого опять же будут находиться в отношении з. с. Разбивая этот меньший пр-к на квадрат и еще меньший пр-к, мы опять получим пр-к з. с., и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют «кривая развития», «спираль жизни», ибо в ней как бы заложена идея бесконечного развития.
 |  |
Бесконечное повторение пр-ка з. с. и квадрата при рассечении пр-ка з. с. обнаруживает повто-рение целого в его частях, что является одним из условий гармонии целого. Это свойство пр-ка з. с. было обнаружено художниками и они стали употреблять з. с. как способ гармонизации, способ пропорционирования. Фидий использовал з. с. при постройке Акрополя (5 век до н. э.) Греческие ремесленники, создавая гончарные изделия также применяли з. с. В эпоху Возрождения з. с. использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли з. с. в поисках гармоничных пропорций букв. (Рис 12),Пр-к з. с. мы встречаем и в пропорциях средневековых рукописных книг, и в современной книге, так как стройные пропорции з. с. позволяют красиво организовать пространство книжной страницы и разворота Пропорционирование — при ведение частей целого к единому пропорциональному строю.В ХХ веке вновь возродился интерес к золотому сечению как к способу пропорционирования. Оно привлекло внимание архитекторов. Советский архитектор Жолтовский и француз Корбюзье занимались проблемами з. с. и использовали его в своей архитектурной практике, Корбюзье создал целую систему пропорционирования на основе чисел ряда золотого сечения и пропорций человеческого тела и назвал ее «Модулор», что по-латыни означает- ритмически размерять Модулор Корбюзье представляет собой гармонические ряды чисел, которые связаны в единую систему и предназначены для использования в архитектуре и дизайне — для гармонизации всей среды, в которой обитает человек. Корбюзье мечтал о перестройке с помощью Модулора всей архитектурной и предметной среды. Сам он создал несколько прекрасных образцов архитектуры, но о более широком применении Модулора в существующих условиях не могло быть и речи. Модулор использовался в ряде слуйаев в дизай¬не и в графическом дизайне — при конструиро¬вании печатных изданий. На рис. 16 приводятся варианты деления прямоугольника 3:4, приведенные Корбюзье для демонстрации возможностей конструирования с помощью Модулора.В разработку вопроса пропорционирования и ис-пользования золотого сечения нес свой вклад Д. Хэмбидж. В 20-м году в Нью-Йорке вышла его книга «Элементы динамической симметрии». Хэмбидж исследовал динамическую симметрию, которую он обнаружил в ряде прямоугольников, с целью ее практического применения художниками в композиционном построении. Он делает попытку раскрыть секреты, которыми пользовались древние греки, добиваясь гармонического решения формы. Его внимание привлекли свойства прямоугольников, составляющих ряд, где каждый последующий прямоугольник строится на диагонали предыдущего, начиная с диагона-ли квадрата Ц2. Это прямоугольники Ц4, Ц5 (с меньшей стороной равной стороне квадрата, принятой за единицу). (Рис. 17). Кульминацией ряда является прямоугольник Ц5, обладающий особыми гармоническими свойствами и «родственный» прямоугольнику золотого сечения, (о нем будет сказано ниже).<


